Newly developed algorithms make it easier to predict the long-term behavior of complex biological systems
19 Dec 2025
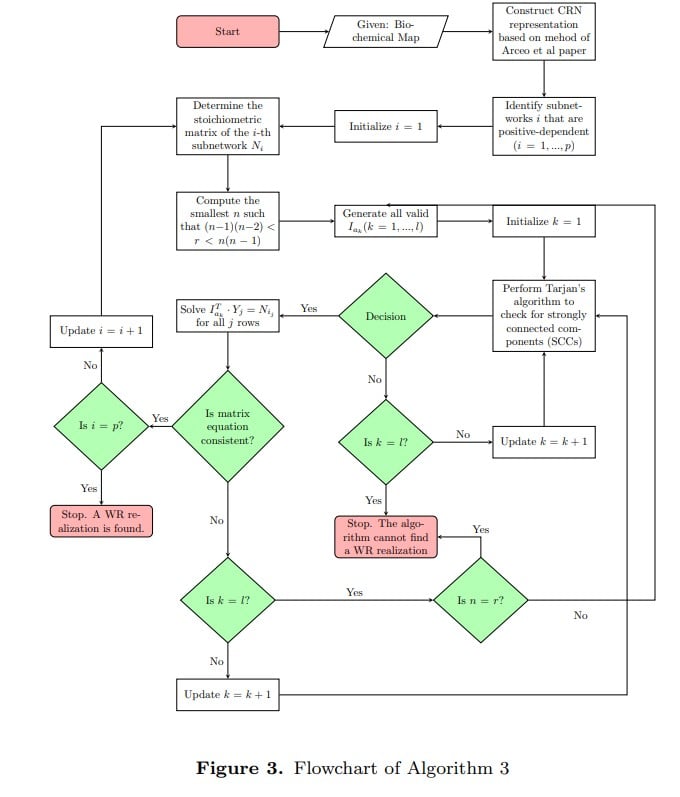
Understanding how complex biological systems work—like how our bodies process nutrients or how the environment balances carbon—requires accurate models. Biochemical Systems Theory (BST) is one way applied mathematicians create these models, using mathematical formulas to describe how different parts of a system interact. However, these models can be difficult to analyze because they often lack certain features that make them easier to study.
Our research solves this problem by developing algorithms that reshape these models into more organized forms called weakly reversible networks. This transformation makes it easier to predict how systems behave over time, especially how they maintain balance and respond to changes. One important result is that some of these new models naturally reach stable states, which is crucial for understanding long-term system behavior.
We applied our methods to models of the Earth’s carbon cycle, which is essential for understanding climate change. Our results showed that these systems can remain stable even when conditions change, highlighting their natural resilience.
This work gives researchers better tools to study biological and environmental systems, leading to potential improvements in health research, environmental management, and sustainability efforts.
This research is significant because it bridges the gap between BST and Chemical Reaction Network Theory (CRNT) by introducing algorithms that transform BST models into weakly reversible reaction networks. Weak reversibility is a critical property that allows researchers to apply powerful CRNT results to analyze system behavior, particularly steady states and stability. By constructing weakly reversible versions of S-systems and General Mass Action systems, this work simplifies complex network structures and validates important theoretical results.
Additionally, the development of deficiency zero networks enables the study of complex-balanced steady states, offering deeper insights into system stability. Applying these methods to carbon cycle models highlights the practical impact of this research, demonstrating concentration robustness—a key feature for understanding environmental and biological resilience. This work not only advances mathematical analysis but also strengthens the modeling of real-world biological and ecological systems.
Authors: Exequiel Jun V. Villejoa (Institute of Mathematics, University of the Philippines Diliman) and Dylan Antonio SJ. Talabis (Institute of Mathematical Sciences, University of the Philippines, Los Baños)
Read the full paper: https://match.pmf.kg.ac.rs/issues/m93n3/m93n3_631-687.html
